![]()
Imaginons que l'on veuille représenter les villes d'une carte géographique comme celle présentée ci-dessous. On peut alors utiliser la technique des arbres qui est d'essence hiérarchique et permet d'effectuer des recherches. Plusieurs types d'arbres sont à considérer. Commençons par les arbres k-dimensionnels destinés à représenter des données dans un espace à k dimensions. La carte géographique proposée correspond à un espace à 2 dimensions. On utilisera donc un "2-d Tree" dont les nœuds comporteront des enregistrements possédant au moins 2 valeurs x et y représentant les coordonnées d'un point sur la carte. Ces enregistrements peuvent posséder aussi d'autres attributs (par exemple le nom de la ville pour reprendre l'exemple illustratif). Comme il s'agit d'un arbre il faut aussi indiquer des pointeurs vers les nœuds suivants. Pour un arbre 2-d, un nœud se présentera donc sous la forme suivante :
![]()
Cela signifie qu'un nœud de l'arbre ne peut avoir que deux descendants au plus, l'un vers la gauche et l'autre vers la droite. La racine de l'arbre correspond au niveau 0. Ses descendants immédiats (2 au plus) définissent le niveau 1, et ainsi de suite.
Par ailleurs, les nœuds sont placés suivant la règle suivante :
Supposons que l'on ait à construire cet arbre pour la carte géographique proposée.
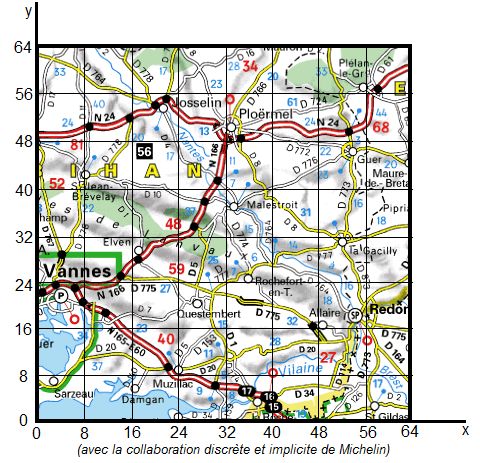
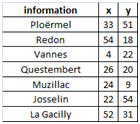
Les villes à prendre en considération sont listées dans le tableau suivant :
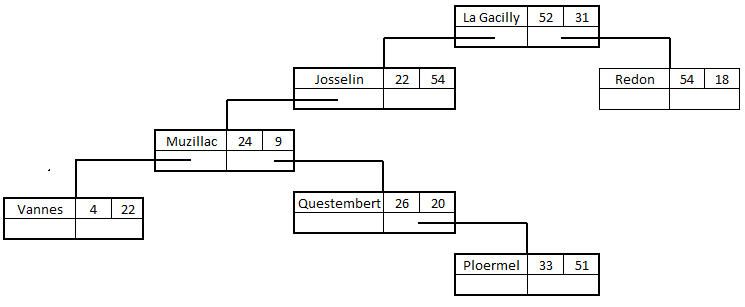
On commence par placer le premier nœud de l'arbre correspondant à la première ville de la liste (niveau 0) :
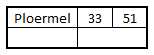
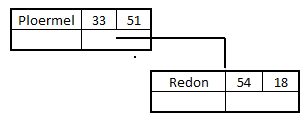
On passe ensuite à la deuxième ville de la liste, Redon (54,18). Comme 54 > 33, le nouveau nœud sera à droite du précédent :
Passons à la troisième ville, Vannes (4,22). On compare d'abord 4 à 33 (de Ploermel) ce qui indique que l'on est à gauche de Ploermel. Comme il n'y a rien à gauche, on place le nœud "Vannes"
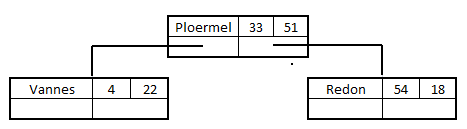
Quatrième ville de la liste, Questembert (26, 20). On compare d'abord 26 à 33 (de Ploermel) ce qui indique que "Questembert" est à gauche de "Ploermel" ce qui nous amène au nœud "Vannes". Puis on compare 20 à 22 (de Vannes) ce qui indique que "Questembert" est à gauche de "Vannes" :
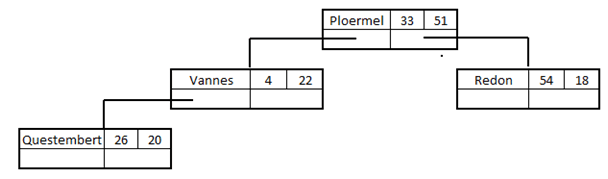
Cinquième ville de la liste, Muzillac (24,9). On compare d'abord 24 à 33 (de Ploermel) ce qui indique que l'on doit aller vers "Vannes". Puis on compare 9 à 22 (de Vannes) ce qui nous amène à "Questembert". Puis on compare 24 à 26 (de Questembert) ce qui nous indique qu'il faut placer le nouveau nœud à gauche de "Questembert" :
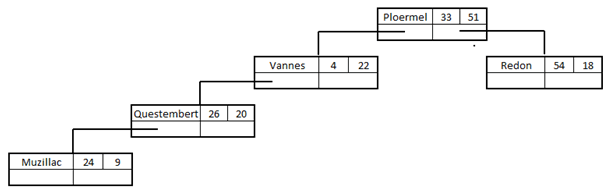
Sixième ville de la liste, Josselin (22, 54). On compare d'abord 22 à 33 ce qui nous amène vers "Vannes". Puis on compare 54 à 22 (de Vannes) ce qui crée à nouveau nœud à droite de "Vannes" :
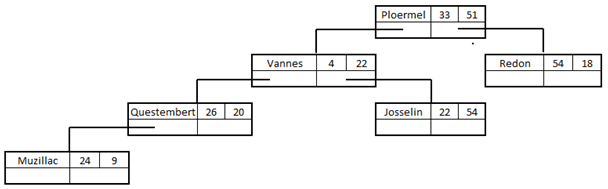
Enfin, septième ville de la liste, La Gacilly (52, 31). On compare d'abord 52 à 33 (de Ploermel) ce qui nous amène à "Redon". Puis on compare 31 à 18 (de Redon) ce qui nous crée un nouveau nœud à droite de "Redon" :
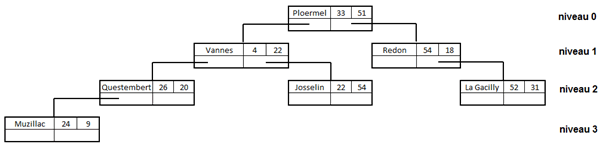
La représentation obtenue est un 2-d Tree à 4 niveaux.
Il est intéressant d'examiner la signification géométrique du processus de construction de cet arbre.
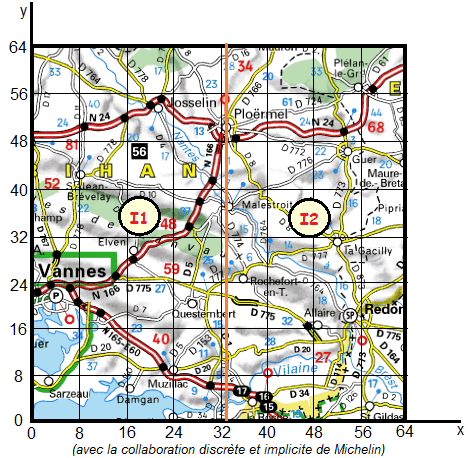
Le premier noeud "Ploërmel" de niveau 0 correspond géographiquement à un point représentant l'image toute entière I. A partir de ce point on peut scinder l'image en deux parties I1 et I2 en traçant la droite verticale x = 33.
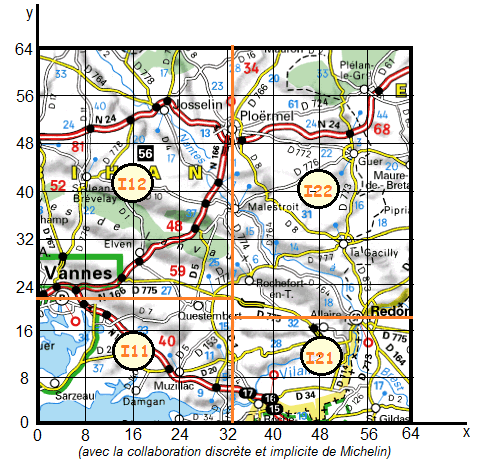
Les deux descendants de "Ploermel", "Redon" et "Vannes" sont au niveau 1. On peut considérer que "Redon" est représentatif de la partie rectangulaire I2 de droite (x ≥ 33) et que "Vannes" est représentatif de la partie rectangulaire I1 de gauche (x < 33). Ces deux nœuds permettent une partition supplémentaire par tracé des droites y = 18 ( I21, I22) et y = 22 (I11 et I12).
Au niveau 3, on a trois nœuds "Questembert", "Josselin" et "La Gacilly". "Questembert" et "Josselin" sont représentatifs respectivement des régions I11 et II2. "La Gacilly" est représentative de la région I22. Aucune ville ne représente la région I21.
Par chacun des points "Questembert", "Josselin", "La Gacilly", on trace des droites verticales d'équations respectives x = 26, x = 22, x = 52, ce qui conduit à un partitionnement supplémentaire I111, I112, I211, I212, I221, I222.
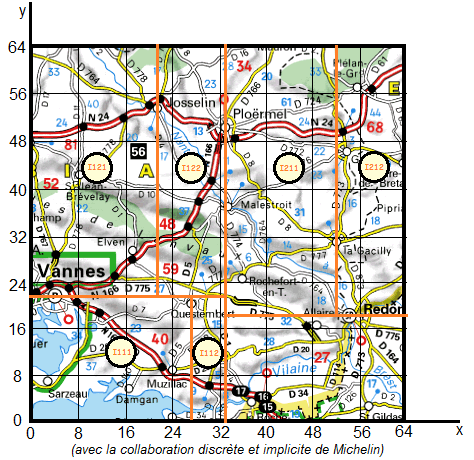
Il ne reste plus que le nœud "Muzillac" de niveau 3, représentatif de la région I111.
On voit donc que l'arbre 2-d Tree correspond à une partition de l'image initiale dont les parties sont de dimensions différentes.
Il faut noter que la construction de l'arbre (et donc le partitionnement de l'image) dépend de l'ordre de la liste des points-villes. Si on renversait la liste précédente, on obtiendrait un 2-d Tree différent :
Dans la méthode des 2-d trees, la partition de l'image s'effectue en traçant soit une ligne verticale (pour les nœuds de niveau pair) soit une ligne horizontale (pour les nœuds de niveau impair). Et chaque nœud possède deux pointeurs @gauche et @droite.
Dans la méthode des quadtrees ou arbres quaternaires, la partition s'effectue en traçant simultanément in ligne verticale et une ligne horizontale, définissant ainsi quatre régions. En conséquence, chaque nœud sera muni de 4 pointeurs @no, @ne, @so, @se, (vers nord-ouest, vers nord-est, vers sud-ouest, vers sud-est) donc chaque noeud peut avoir au plus 4 descendants :
![]()
Appliquons la méthode en reprenant la liste des villes précédentes.
Placement de "Ploërmel" : c'est le premier nœud, racine du quadtree
|
|
Placement de la deuxième ville, Redon (54, 18). Cette ville se trouve dans la région I4 (sud-est). On placera le nœud correspondant comme pointé par @se :
Le point correspondant sur la carte permet de subdiviser I4 en 4 parties I41, I42, I43, I44 |
|
Placement de la troisième ville, Vannes (4,22). Cette ville se trouve dans la région I3. On plera donc le nœud correspondant comme descendant du nœud "Ploermel" via le pointeur @so :
|
|
Placement de la quatrième ville, Questembert (26, 20). Cette ville est située dans la région I34, au sud est de Vannes. Le nœud correspondant sera donc un descendant de Vannes via le pointeur @se :
|
|
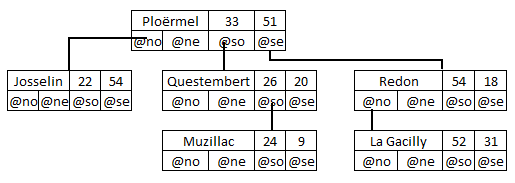
En continuant ainsi pour les villes restantes, on aboutit à l'arbre suivant et au découpage correspondant de la carte :
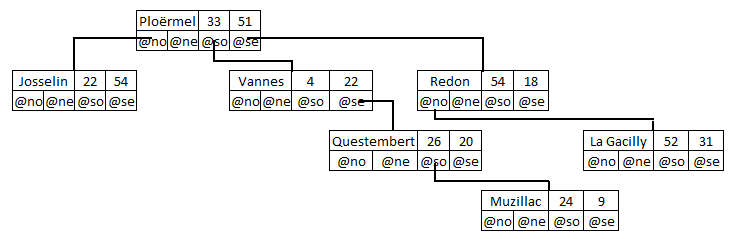
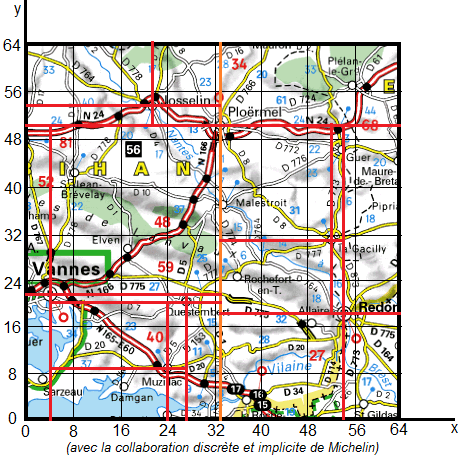
Cette méthode présente le même inconvénient que le 2-d Tree : si l'on change l'ordre des villes on obtient un arbre et un découpage d'image différents.
Comme on a pu l'observer dans les deux types d'arbres précédents, le découpage géographique en région est "irrégulier" et dépend de l'ordre de placement des points dans la liste. Suivant l'ordre utilisé, l'arbre peut être plus ou moins "haut" ou "profond".
Les arbres MX-Quadtrees correspondent au contraire à un découpage régulier mais nécessitent de partir d'une image carrée dont les dimensions sont 2kx2k. Le choix de k influe sur la granularité du découpage. Le noeud racine correspond à l'image toute entière. Celle-ci est divisée en 4 parties égales en traçant les droites x = 2k/2 = 2k-1 et y = 2k/2= 2k-1. Chacune de ces 4 parties correspond à un noeud descendant du noeud racine. A leur tour, elles sont divisées en 4 parties et ainsi de suite :
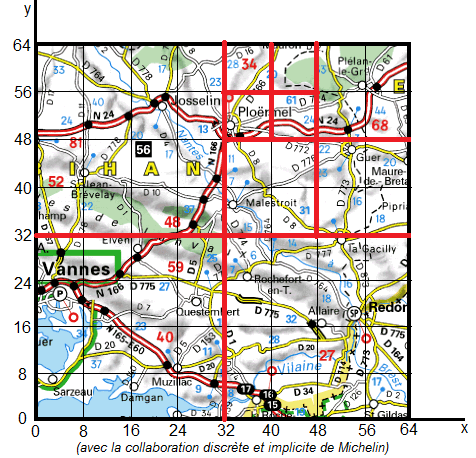
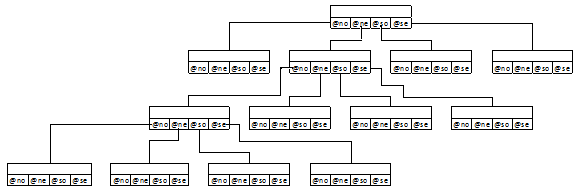
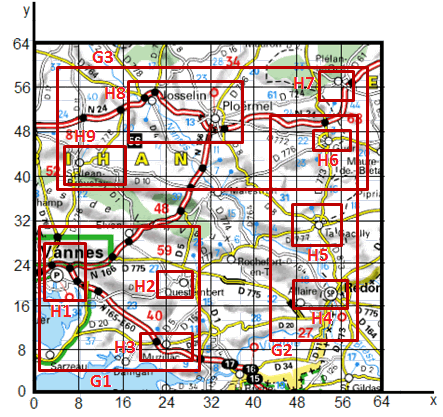
Pour localiser les villes utilisées dans la liste précédente, il faudra effectuer le découpage suivant :
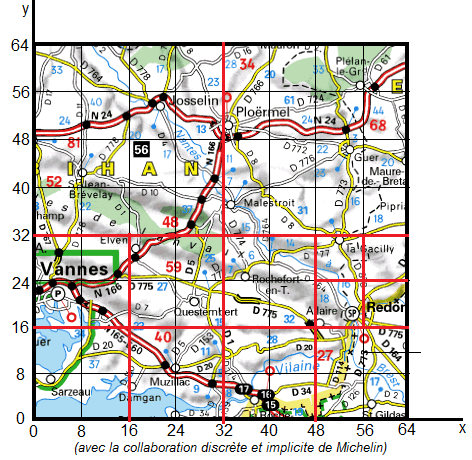
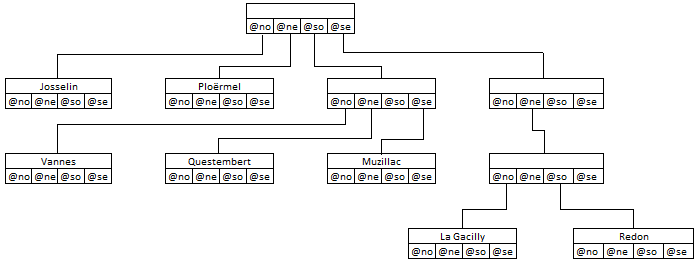
Implicitement dans le schéma précédent, nous avons restreint les régions à la présence d'un point. Par exemple Josselin est dans une grande région par rapport à Redon. Si on voulait ajouter la ville Saint-Jean Brevelay, il faudrait alors découper la région de Josselin en 4 parties de manière à ce qu'une région ne corresponde qu'à une seule ville. Bien entendu, on pourrait effectuer le découpage total en carrés de côté 20 = 1, mais cela correspondrait à stocker des noeuds vides et gaspillerait de la place mémoire.
Le codage d'un MX-Quad-Tree est assez simple. Il faut d'abord se fixer une règle : NO = 0, NE = 1, SE = 2, SO = 3. Il suffit alors de mettre à la suite les numéros de quadrants pour obtenir le codage. On normalise ensuite en mettant X là où il n'y a pas de point significatif. Pour l'exemple précédent, on obtient : 0X (Josselin), 1X ( Ploermel), 30X (Vannes), 31X (Questembert), 32 (Muzillac), 210 (La Gacilly), 213 (Redon).
Les arbres R-Trees sont très différents des précédents. Ils consistent à stocker des rectangles pouvant contenir à leur tour d'autres rectangles. Les feuilles de l'arbre sont des rectangles. Les noeuds intermédiaires sont des groupes de rectangles.
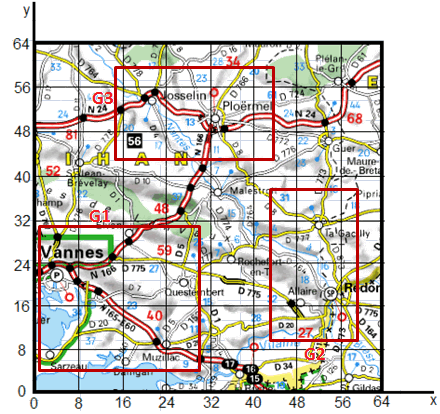
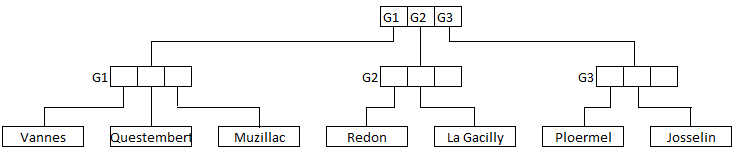
Les R-trees obéissent toutefois aux règles suivantes :
L'arbre du schéma précédent est d'ordre K = 3.
Nous examinons ici comment effectuer des recherches dans un arbre comme ceux des types précédents. La mise à jour des structures précédentes constitue, par ailleurs, un point crucial de choix. Par mise à jour on entend ici l'insertion et la suppression de noeuds.
k-d Trees
Le recherche d'un noeud s'effectue simplement en suivant les règles qui ont permis de construire l'arbre. Toutefois, le type de recherche le plus intéressant est celui où on veut sélectionner les points qui se trouvent à une distance inférieure ou égale à une valeur r d'un point donné (x0, y0). Par exemple, on recherche les villes qui se trouvent à proximité du point (24,16) dans un rayon de 8 unités. Elles se trouvent dans le cercle rouge ci-dessous : on constate que Questembert et Muzillac répondent à la requête.
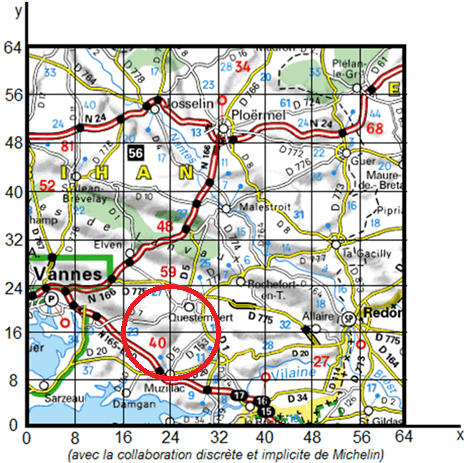
Pour arriver de manière automatique à ce résultat, on est amené à compléter la structure d'un enregistrement en ajoutant les bornes des régions représentées par les points. On ajoutera ainsi dans chaque noeud N, xmin(N), xmax(N), ymin(N), ymax(N). Par exemple pour Redon et Vannes, on aura les enregistrements suivants :
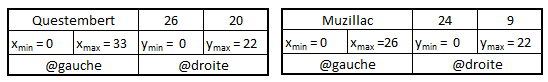
En se basant sur ces paramètres supplémentaires, la requête consiste à rechercher les intersections des régions représentées par les noeuds avec le cercle de rayon r. On parcourt le 2-d Tree pris comme exemple initial en commençant par la racine (Ploërmel) qui ne correspond pas à un point du disque d'équation (x - 24)2 + (y - 16)2 ≤ 64. On passe ensuite à ses descendants :
Le résultat de la requête est donc {Questembert, Muzillac}.
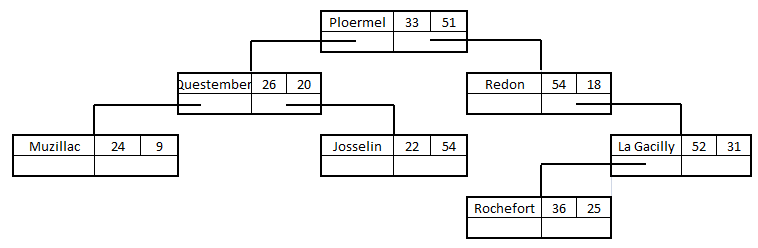
L'insertion d'un nouveau noeud ne pose pas de problème. Par exemple ajoutons la ville Rochefort-en-Terre (36, 25). En comparant les x et les x aux noeuds présents, on constate que le nouveau noeud prend sa place comme descendant gauche de La Gacilly :
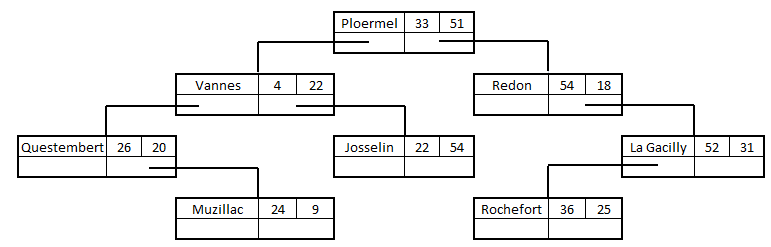
La suppression est plus complexe lorsque le noeud n'est pas une feuille de l'arbre, mais un noeud intermédiaire dans la mesure où ce noeud peut avoir des descendants qu'il faut, eux, conserver. Ces descendants, et leurs descendants, constituent des sous-arbres qu'il va falloir raccrocher à des noeuds restants. Supposons que l'on supprime le noeud "Vannes". Nous avons à replacer deux sous-arbres, celui qui a pour racine "Questembert" et celui qui a pour racine "Josselin". L'arbre de gauche, de racine "Questembert", sera raccroché à Ploërmel à gauche. On ne peut évidemment faire de même avec le sous-arbre de droite constitué du seul noeud "Josselin".Il faut réorganiser l'arbre ce qui est couteux en temps :
QuadTrees
La recherche de points au voisinage d'un point donné se traite de la même façon que pour les 2-d Trees : on élimine les sous-arbres dont la racine représente une région qui n'a pas d'intersection avec le disque cible. Plus précisément on utilise l'algorithme récursif suivant :
procedure Recherche( T noeud, C cercle)
{
Si region(T)∩C = ∅
alors stop;
sinon
si (x(T), y(T) ∈ C alors lister le noeud;
procedure Recherche (@no(T), C);
procedure Recherche (@ne(T), C);
procedure Recherche (@so(T), C);
procedure Recherche (@se(T), C);
FinSi
}
Pour l'insertion, le procédé a été vu lors de la construction d'un arbre.
Pour la suppression d'un noeud, le procédé est aussi délicat que pour le cas des 2-d Trees. Par exemple si l'on veut supprimer Vannes de l'arbre obtenu précédemment, on aura la reconstruction suivante :
MX-Quadtrees
Nous avons vu l'insertion des noeuds en construisant précédemment l'arbre.
La recherche de localisation de villes par rapport à un point donné est analogue aux cas précédents avec deux différences :
Cette dernière remarque explique aussi pourquoi la suppression est ici ultra simple : les noeuds représentatifs des points n'ont pas de sous-arbre. On peut donc les supprimer sans avoir à reconstruire l'arbre.
R-Trees
La situation est ici radicalement différente des précédentes.
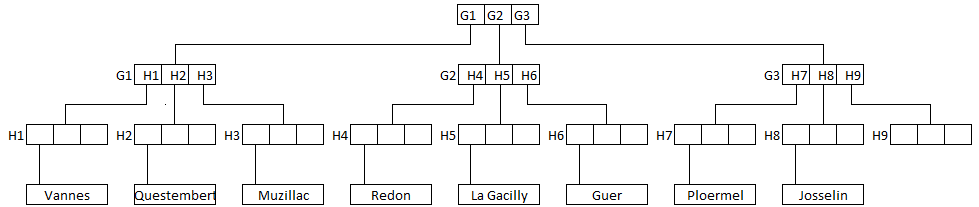
Pour l'insertion d'un nouveau rectangle, il faut tenir compte de la règle suivant laquelle un rectangle doit contenir au moins K/2 rectangles et au plus K rectangles. Cela veut dire que lorsqu'il y a encore de la place dans un rectangle on peut incorporer éventuellement le nouveau rectangle. Par exemple ajoutons Plélan le Grand, Guer et Saint-Jean Brévelay. Il n'y a que deux places disponibles. Il faut donc ajouter un niveau et répartir les villes de manière à ce qu'un noeud soit au moins à moitié rempli. On pourra adopter le découpage suivant qui correspond à l'apparition d'un nouveau niveau (pour k = 3).

La suppression doit aussi tenir compte de la règle de remplissage : entre K/2 et K rectangles. Par exemple si l'on supprime Plélan le Grand et Saint jean Brévelay, le rectangle G3 ne contient plus assez de rectangles intérieurs. Il faut alors reconstruire l'arbre (la règle n ≥ k/2 ne s'applique pas aux feuilles) en essayant de lui donner un aspect équilibré.
Choisir la bonne réponse dans les questions suivantes. Une bonne réponse rapporte 1 point, une mauvaise - 1 point. Le choix d'une réponse n'est pas obligatoire. Il peut y avoir plusieurs bonnes réponses.